fx-991 CN X发布于2014年，第一批产品也已经过了十岁生日。fx-991 CN X的针对用户为高中、大学生。实际上，fx-991 CN X作为一款定位较为高端的函数计算器，它的使用人群已经超过了高中、大学生的范围。此次卡西欧专门推出针对社会人士的系列，其原因是很值得一探究竟的。本文将展示两款计算器不同的外观，并比较两者在实际操作过程中的区别。
外观设计
本次更新的函数计算器都采用了全新设计的模具。fx-999 CN CW放弃了上一代的一体化模具，其正面板的边缘可以看到一条较大的缝隙。
两台计算器都是中山工厂制造。
CW系列主打用户友好。可以看到，fx-999 CN CW的正面板被极大地简化：按键的数量减少，并且全部变成了圆形；个人认为fx-991 CN X的方形（输入键区，含OPTN）和圆形按钮（主控键区）搭配设计是有一定层次感的，而fx-999 CN CW将所有按钮改为圆形则更符合较为内敛的纯色设计。
滑盖设计变为卡扣设计。这个保护盖比较有型，背面是磨砂质感的，有点像手机壳。
fx-999 CN CW提供黑白两色可选，配色方案没有fx-991 CN系列那么丰富。
界面与操作
界面变化
计算器的操作界面发生了较大的变化。第一是引入了四级灰度。这个功能唯一实用的地方就是用来高亮正在输入的内容。当用户正在输入较为复杂的公式时，正在输入的部分会用深灰度标记，其他部分会变为浅色，这样一来可以达到一个聚焦的效果。但笔者认为这样不利于检查公式已经输入的部分，不能叫做锦上添花。
有四级灰度的加持，主屏幕的审美也升了一个量级。
第二个直观感受就是界面字体变了。这个字体有一点点像非衬线体，看起来比较硬朗，笔画分明，没有fx-991 CN X的字体看起来那么圆润，搭配四级灰度显示非常犀利。
新的提醒界面放上了一个警告标示，特别醒目，同时在底部弄了个“返回”的高亮条，去掉了fx-991 CN X的取消选项。
新的功能键区
由于主面板按键数量被精简，fx-999 CN CW在操作方式上跟fx-991 CN X有较大的区别。主面板上一些原有的功能被迁移至了“工具”菜单。这个“工具”菜单类似于原来的OPTN键。
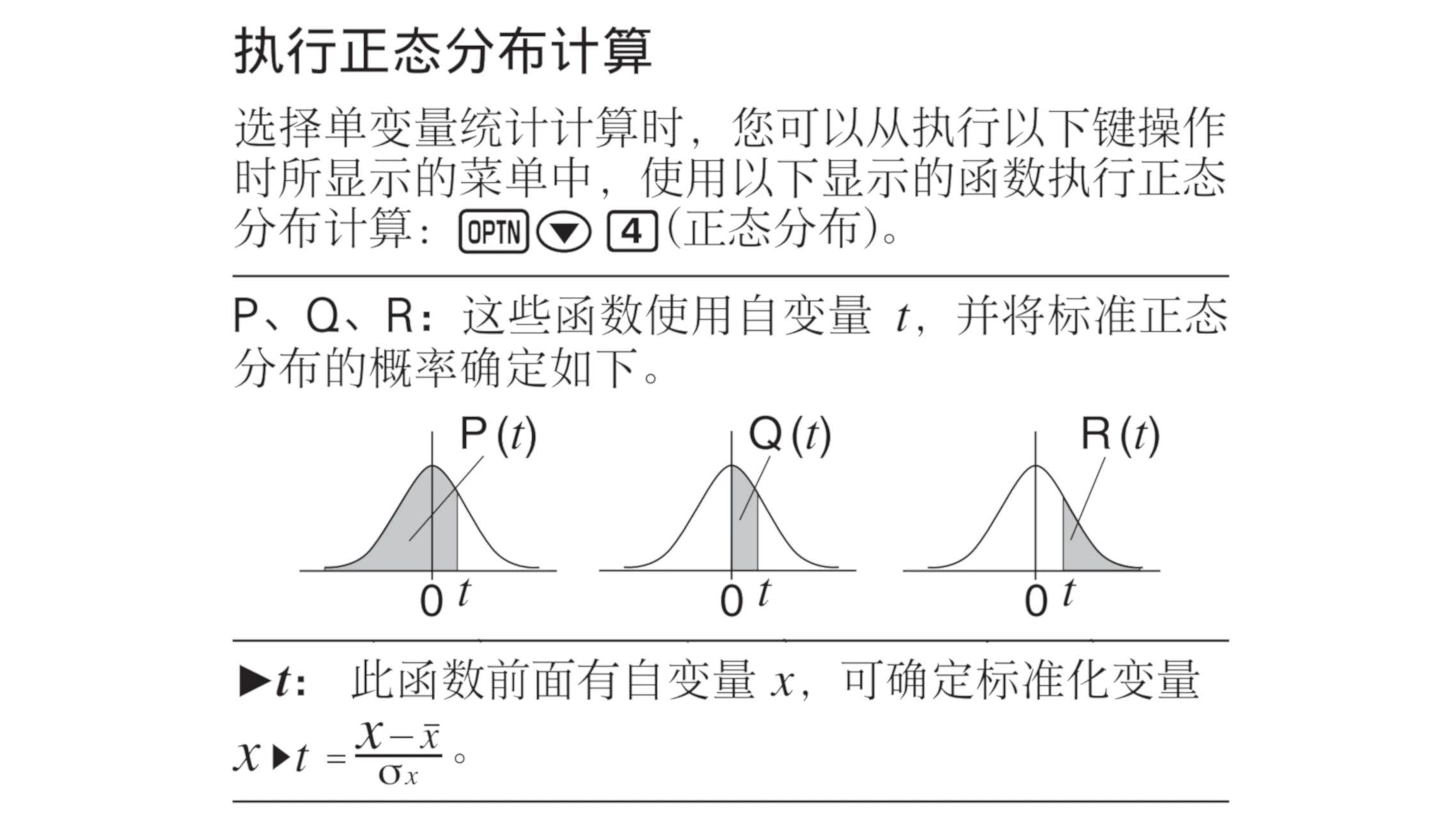
新增“函数”键与“功能”键。新增的全局函数功能可以在计算器的任何数值输入区域内使用$f(x)$及$g(x)$定义符，计算时调用用户自定的函数解析式。“变量”键相当于之前的的STO键，可以展示出目前变量的赋值情况。
当然，“变量键”还有一个很有意思的功能：当计算器界面上的任何一个数值元素处于高亮状态时，按下“变量”键，选择“赋值”便可直接修改变量值。
数字选择被取消
fx-999 CN CW的菜单内是无法使用数字选择的。要想选中操作项，只能使用屏幕下方的方向键组移动。卡西欧还在其右下方提供了长条形的快速翻页按钮，能够直接到达目录下一页的页首或页尾。
其他的一些小变化
新计算器底部还有一个“格式”按钮。按下这个按钮，可以将屏幕上的各种数字形式转化至分数、小数、六十进制形式等等，集成了fx-991 CN X中[S⇔D]和ENG键分别对应的功能。
还能看到，在计算器的右下角，等号键被重命名成了“EXE”键，即执行（execute）键。fx-991 CN X上，等号键兼有“确定”的功能。这点跟fx-CG50倒是很相似。
操作实例
为了对比两款计算器的各方面差异，笔者将用一些例题测试。这些例题仅用于反映fx-999 CN CW的新功能和fx-991 CN X在没有该功能下的替代方案，不完全具有实用价值。其中的一些操作方式由笔者的操作习惯决定。
电子表格由于是首次出现在国行机的新功能，并且它的使用十分灵活，故其不在本文的讨论范围内。笔者会考虑日后单独就这一功能进行补充说明。
数值运算——简单求和与定积分计算
例题I：计算$\int_0^{500} x^2,dx \cdot \sum_{i=1}^{500}{x^2}$。
在fx-991 CN X上：
首先输入积分符号。按下[设置]键下方的积分键，输入表达式$x^2$；向右移动光标，输入积分的下限和上限；再向右移动光标，退出积分编辑，完成对定积分的输入。
其次需要输入求和符号。按下计算器左上方的SHIFT键，选择开机键下方的$x$键（上方标有$\sum$符号），输入待求和的公式，输入完毕后按下右方向键，光标自动定位至自变量区域。输入$1$，按下上方向键，输入$500$，再向右移动光标完成对公式的输入。
按下[=]键。计算器在一段时间的清屏状态后，给出了最终答案$1.741322917\times10^{15}$。
在fx-999 CN CW上：
积分符号输入过程基本同fx-991 CN X一致，仅存在一部分键位差异。
由于求和符号并不在计算器面板上，因此需要按下计算器上方的“目录”键调出这个函数。其次选择“函数与分析”，并按下EXE或OK键确认。使用方向键向下翻动，选择“求和”并确认。与fx-991 CN X不同的是，在输入完求和符号后，光标并不会自动移至求和符号公式区域，所以我们需要按一下左光标键，进入求和函数内的公式输入模块。输入完函数后按下右光标键退出求和编辑，再按下[EXE]键。
总结：
fx-999 CN CW精简面板带来的后果是输入较以往会徒添一些步骤，对于以前使用fx-991 CN X的用户来说可能会感到不适应。习惯以后这种不适感稍加缓解。
线性代数应用——求逆矩阵
例题II：计算该矩阵的逆矩阵：
$$ \begin{bmatrix} 1 & 9 & 5 \\ 8 & 1 & 0 \\ 4 & 9 & 4 \end{bmatrix} $$在fx-991 CN X上：
按下菜单键，再轻按数字键区的“4”（或者将光标移至“4:矩阵”），进入矩阵模式。系统会询问是否需要定义矩阵，此时需要按“1”键选择定义矩阵A（MatA），连按两个“3”表示我们正在初始化一个三行三列的矩阵，接着再一次输入矩阵中的数字。最后按下等号键退出矩阵编辑视图。
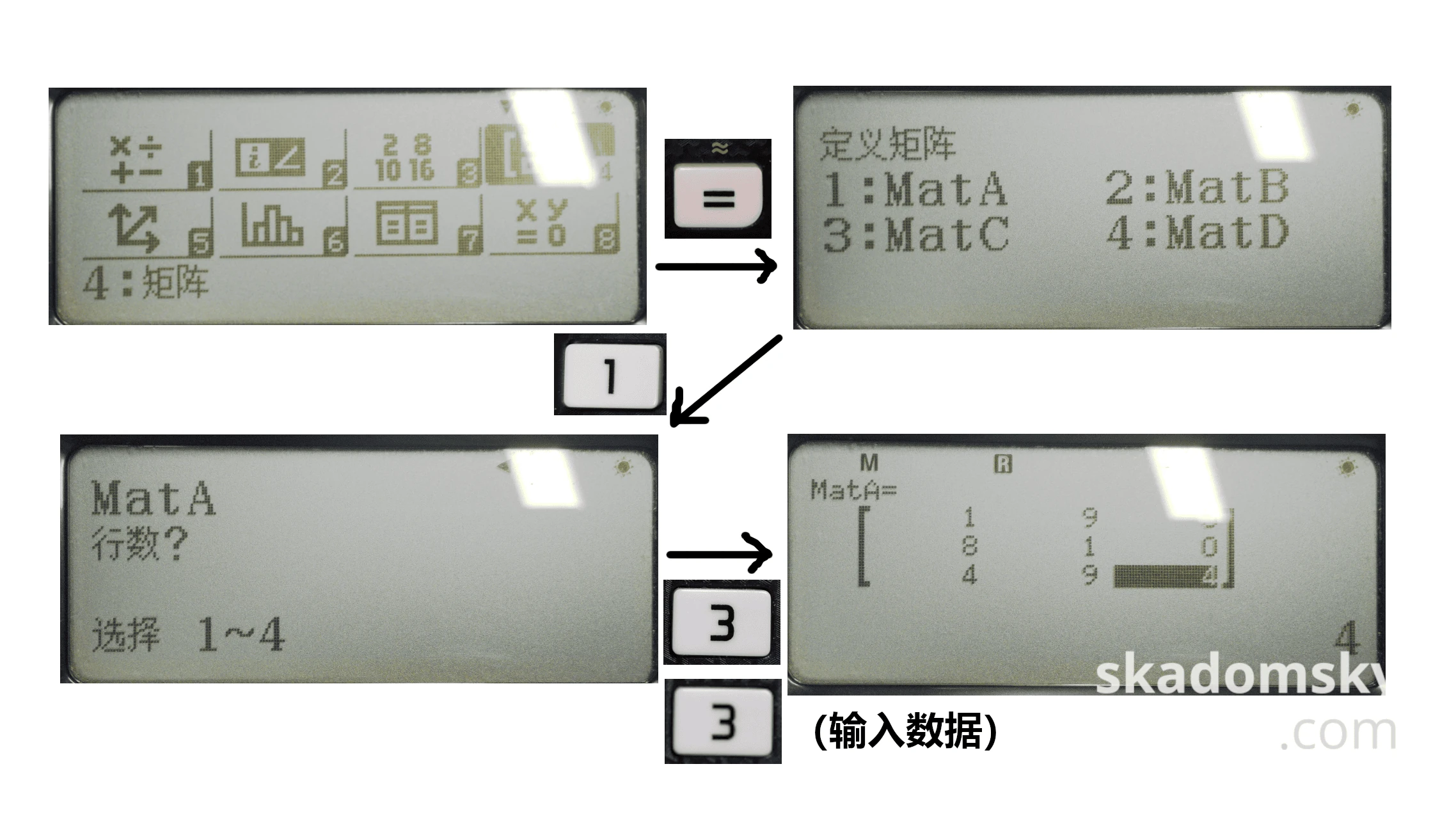
按下OPTN键，调出选择菜单。选择MatA，再按下面板上的[-1]键，按下[=]键，屏幕上显示的MatAns即为所给矩阵的逆矩阵。
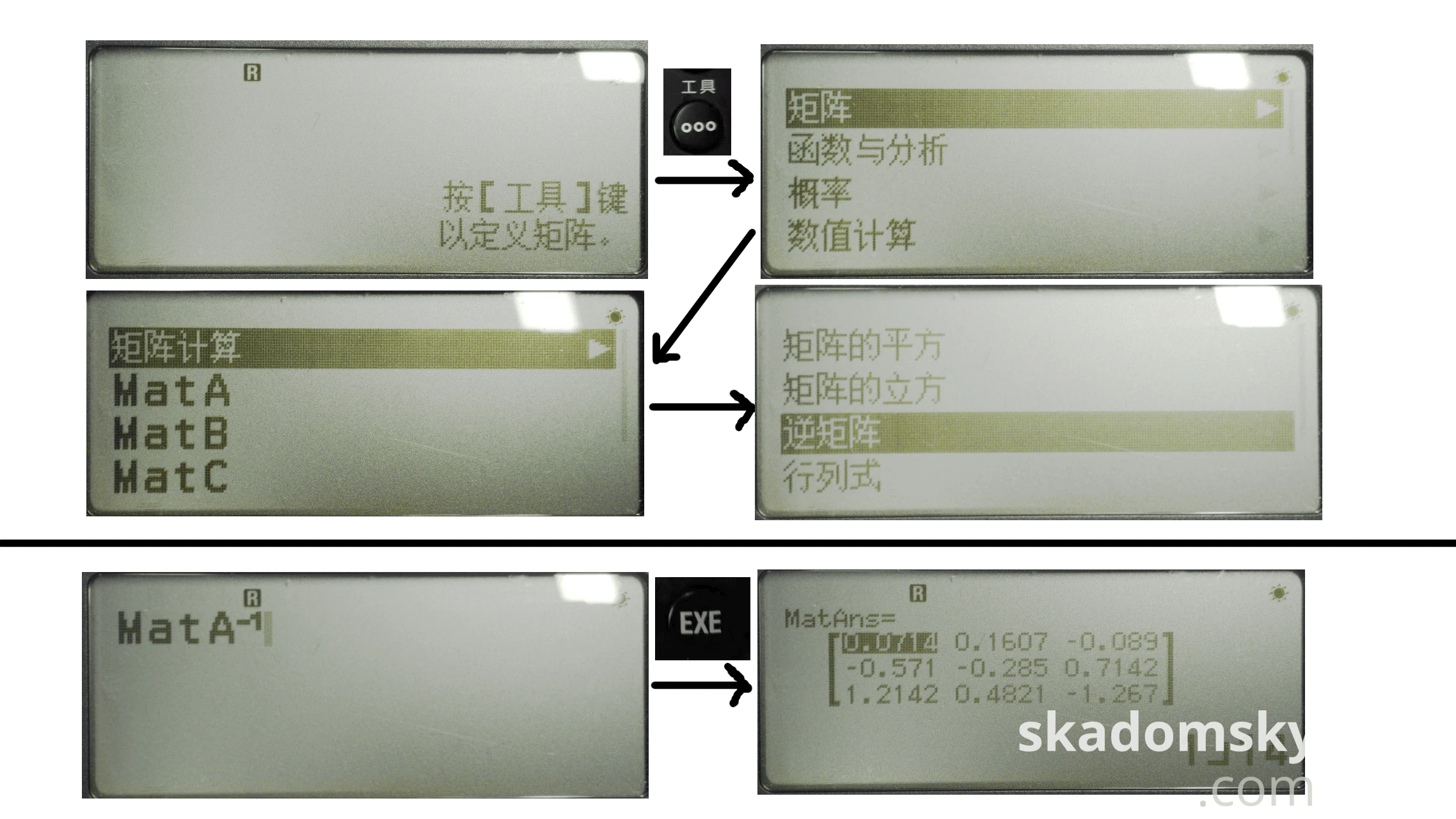
在fx-999 CN CW上：
按下计算器键盘左上角开机键旁边的“主屏幕”键，操作方向键使得“矩阵”模块属于高亮状态，再按下OK或EXE键进入矩阵模式。与fx-991 CN X不同的是，fx-999 CN CW在进入矩阵模式时并不会询问我们是否需要定义新矩阵，而是提示我们需要按[工具]键以定义矩阵。
按下工具键，选择MatA进行定义，使用方向键在接下来的视图中对行数和列数进行编辑，最后将光标移动至下方的“确认”，输入矩阵内部参数，完成对MatA的定义。
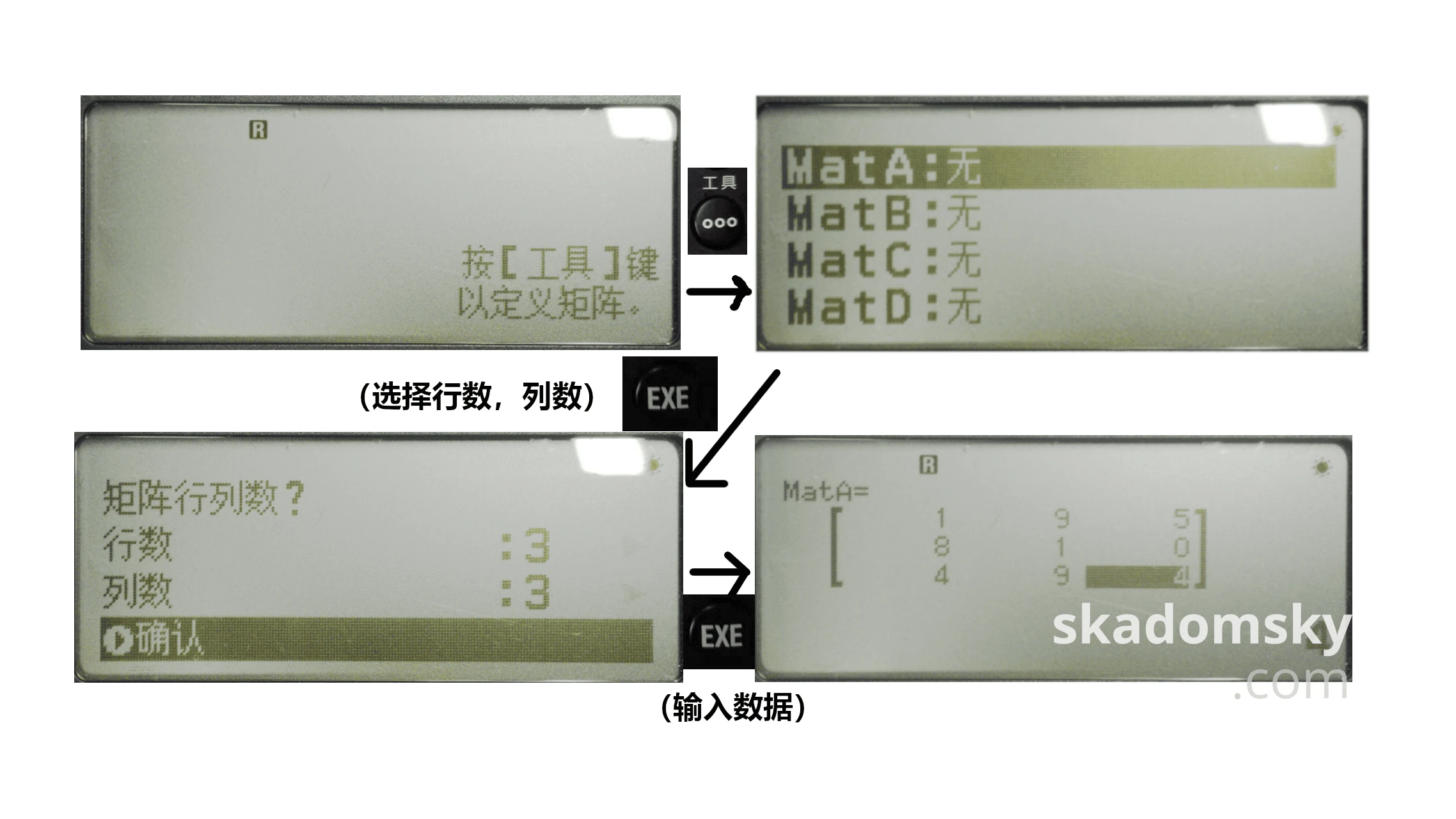
在fx-999 CN CW上，既可以在[菜单]中选择逆矩阵选项也可以直接按下[-1]键对矩阵求逆。输入完求逆运算符后，按下[EXE]键，结果即为上述矩阵的逆矩阵。
总结：
说实话，fx-999 CN CW将一部分功能整合在二级菜单里的做法也不是毫无道理可言的。对于fx-991 CN X用户而言，这个操作大大增加了操作的时间。但对于刚使用计算器的新手而言，这种设计其实更有利于发现新功能。
概率论应用——离散与连续性随机变量分布求参数
例题IV：已知随机变量满足$X\sim B(6,\frac{1}{3})$，求$P(X\le2)$。
在fx-999 CN CW上：
按下“主屏幕”键，进入[分布]模式，选择二项累积分布，再选择“变量”。
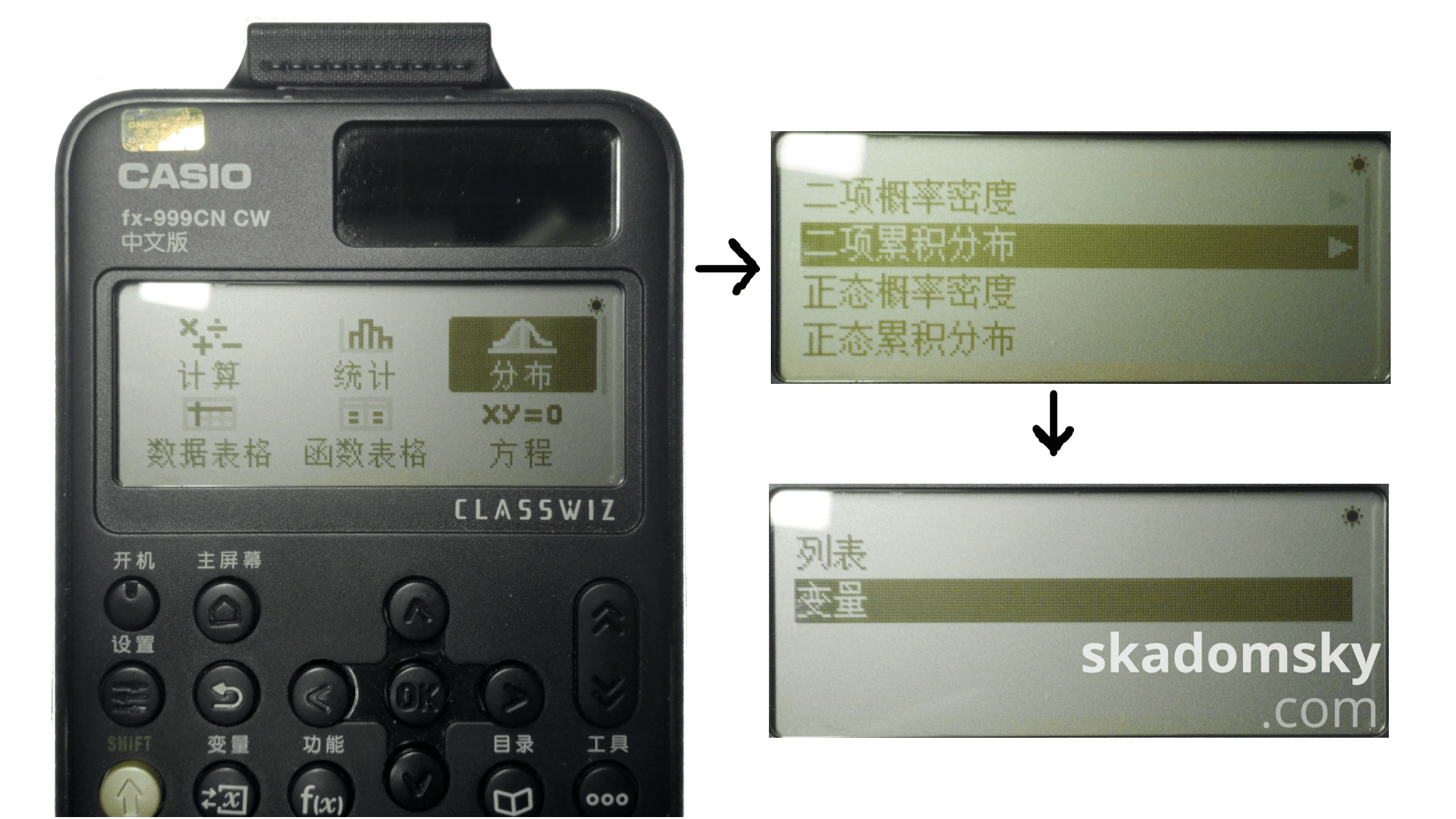
此处可以直接输入二项分布的各个参数。依次输入完参数（x,N,p）后，将光标移至[执行]按钮，按下[OK]或[EXE]键开始执行分布运算。
计算器在较短的时间内得出了答案：$P=0.6803840878$。
在fx-991 CN X上：
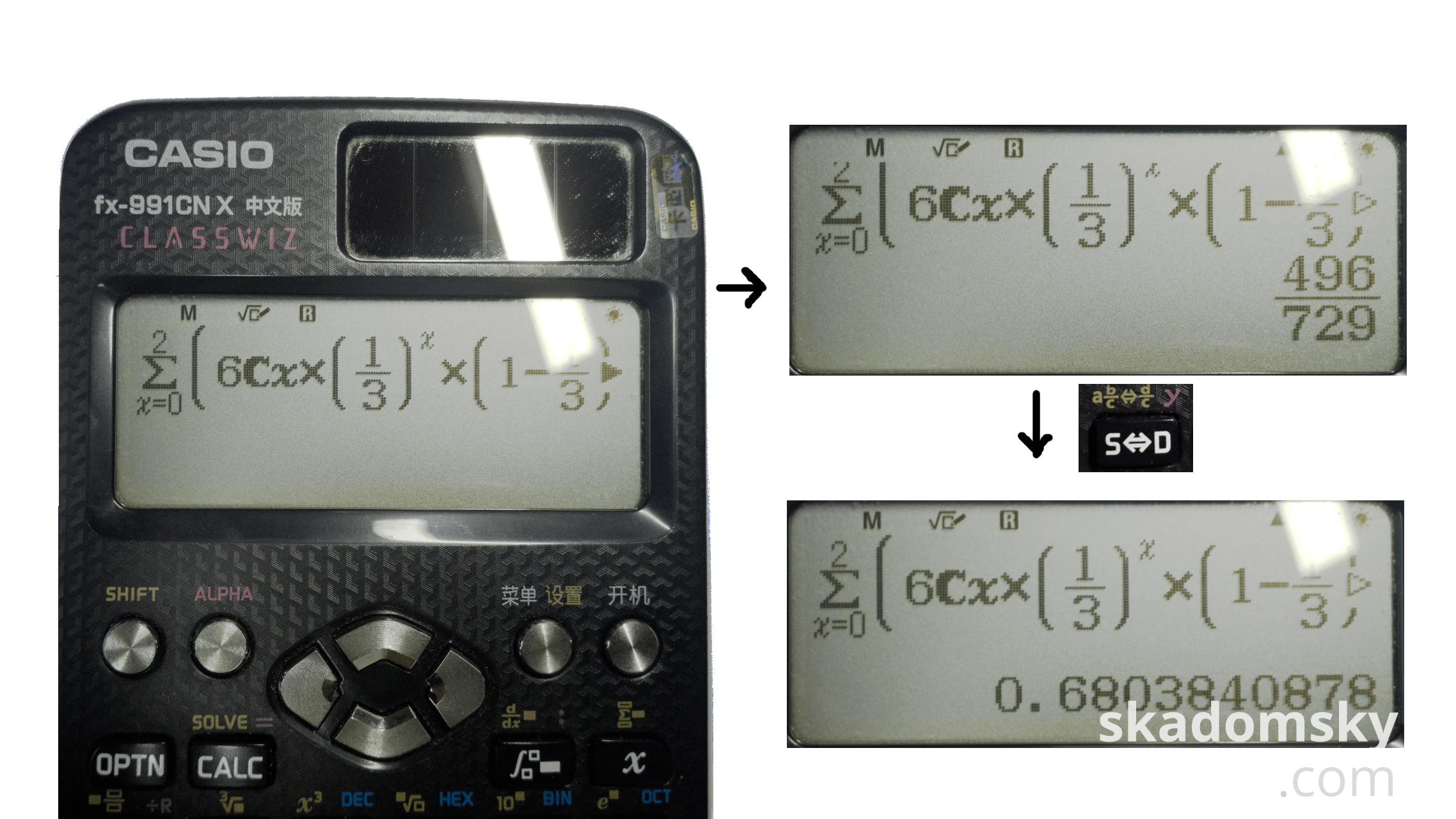
进入数值计算模式。根据二项分布中概率的计算公式及离散型随机变量累计概率的计算公式：
$$ P(X=k)=\binom{n}{k}p^{k}(1-p)^{n-k} $$ $$ P(X\leq k)=\sum^{k}_{i=0}P(X=i) $$使用求和功能计算。输入公式：
$$ \sum^2_{x=0}(6Cx\times(\frac{1}{3})^x\times(1-\frac{1}{3})^{6-x}) $$最后按下[=]键，计算器在大约一秒钟的时间内给出了最后的答案：$\frac{496}{729}$. 按下[S<=>D]键换成小数，得到了与fx-999 CN CW相同的答案：$0.6803840878$。
总结：
fx-999 CN CW新添的“分布”功能允许用户直接输入参数来完成分布概率密度计算。比起fx-991 CN X，其优势主要体现在计算概率密度时完全不用输入计算公式，节约了输入公式的时间。当然，如果想要在fx-991 CN X上直接输入参数完成概率密度计算，输入完概率密度的计算公式后，可以使用公式求解的功能：
二项分布涉及两个变量，此处以变量$y$替代$N$，变量$B$替代p变量$C$替代$k$（这个$x$是二项分布里的参数，不是计算器求和符号下面的指标。这个变量名称是计算器固定的，并且只影响求和符号内部的计算。）如此，可以将上方的公式修改为：
$$
\sum_{x=0}^{C}(yCx\times B^x\times (1-B)^{y-x})
$$
按下[CALC]键，计算器屏幕底部会出现一个高亮条，提示我们为变量提供值。
输入6作为变量$y$的值，按下向下移动的方向键；$x$不是自变量，不需要我们赋值，按方向键跳过；B为概率，输入$\frac{1}{3}$；C为变量上限，输入$2$。
最后按下等号键，计算器给出了如上相同的答案。
另外，二项分布经常涉及大量的二项式计算，有时在fx-991 CN X上直接输入公式计算会出现预防系统内存溢出的“数学错误”提示界面。相比之下，fx-999 CN CW的“分布”模块很明显采用了更快的数值方法。
例题V：已知随机变量$X$服从标准正态分布，求$P(-1\le X \le 3)$。
在fx-991 CN X上：
由正态累积分布公式可知
$$
P(a<X<b)=\int_{a}^{b}\frac{1}{\sigma\sqrt{2\pi}}{e^{-\frac{(x-\mu)^2}{2\sigma^2}} }
$$
将$a$与$b$替换为积分下上限，$\mu$和$\sigma$替换为$0$和$1$，按下等号键执行计算，得到答案$P=0.839994848$。
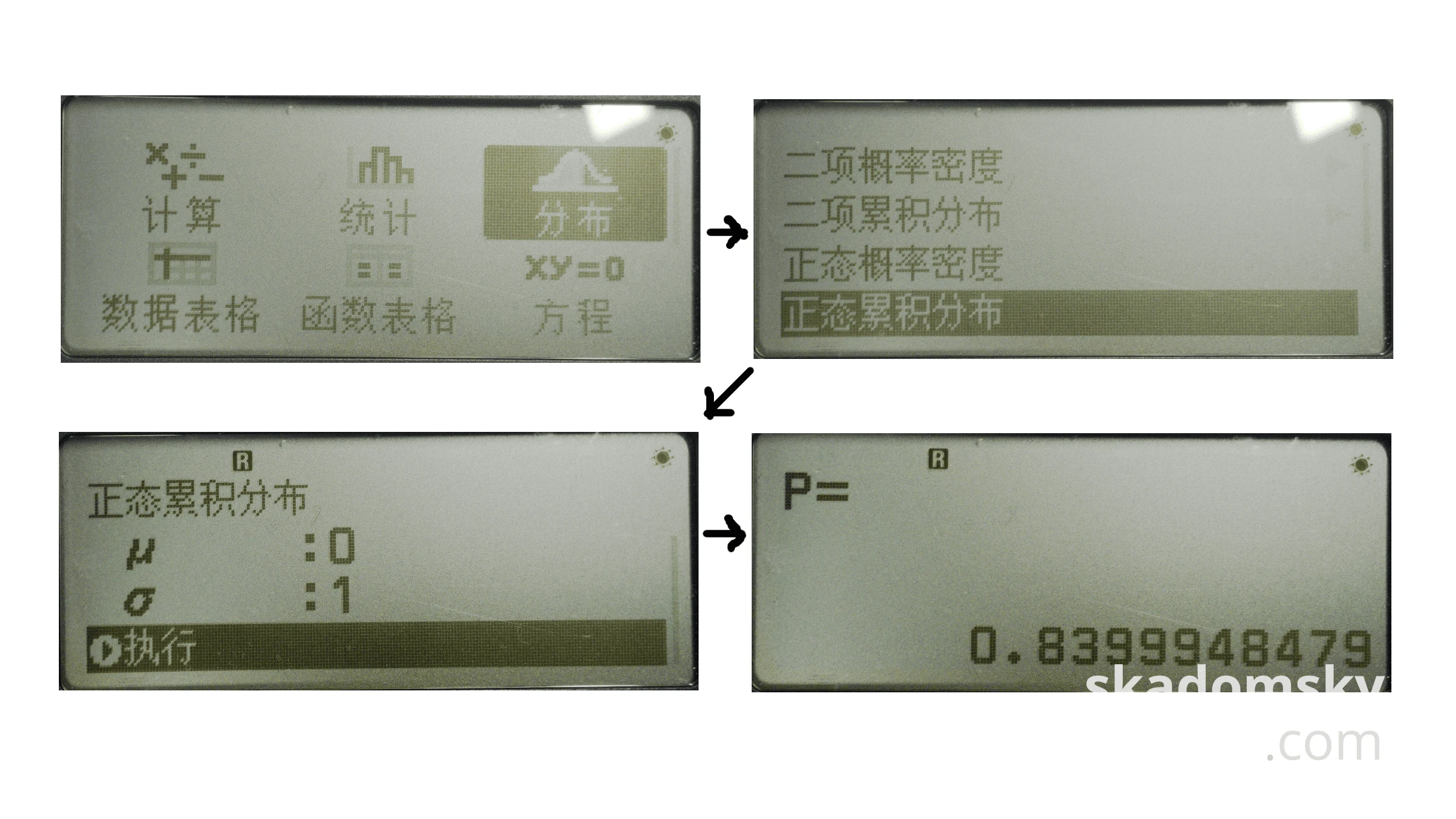
在fx-999 CN CW上：
切换至“分布”模式，选择“正态累积分布”，输入积分下上限$-1$和$3$，再输入标准正态分布参数$\mu =0,;\sigma = 1$，将光标移至“执行”键，得到小数点后还精确一位的答案$P=0.8399948479$。
总结：
fx-991 CN X的统计功能下就已经有了正态分布的功能。由说明书中得知，用户可以在单变量统计模式下输入统计数据，计算器会自动求得均值、方差，然后使用内置函数进行计算：
而fx-999 CN CW新添的“分布”功能则允许用户直接输入参数来完成分布累计计算。对于除反正态分布外的其他分布，fx-999 CN CW均提供对应的概率密度函数（PDF）以及累计分布函数（CDF）。甚至可以使用“列表”功能向计算器输入多个变量求出其分别对应的概率，类似fx-991 CN X的CALC功能。
解积分上下限含有未知数的定积分方程
例题VI：求解$x^3+1+x\sqrt{1+x^2}=\int_{0}^{x}{2x^3}dx$。
在fx-991 CN X上：
根据牛顿-莱布尼茨公式（微积分基本定理）$\int_{a}^{b}f(x)=F(b)-F(a)$，对方程式右边进行展开：
$$
\int_{0}^{x}2x^{3}dx=\frac{1}{2}x^4-0=\frac{1}{2}x^4
$$
原方程即化为
$$
x^3+1+x\sqrt{1+x^2}=\frac{1}{2}x^4
$$
使用牛顿迭代法对该方程进行求解。进入“计算”模式，输入方程式，按下SHIFT+CALC调用SOLVE功能。笔者在这里选用$1$作为迭代的初始值，按下等号键后稍等片刻，计算器便给出了最终的答案：$-0.606473274$。
在fx-999 CN CW上：
与fx-991 CN X不同的是，fx-999 CN CW迭代法解方程（即SOLVE功能）并不在“计算”模式下，而是被迁移到了“方程”模块下。进入方程模式，选择“求解方程”，输入题目中所给出的方程，并给定初始值，执行。
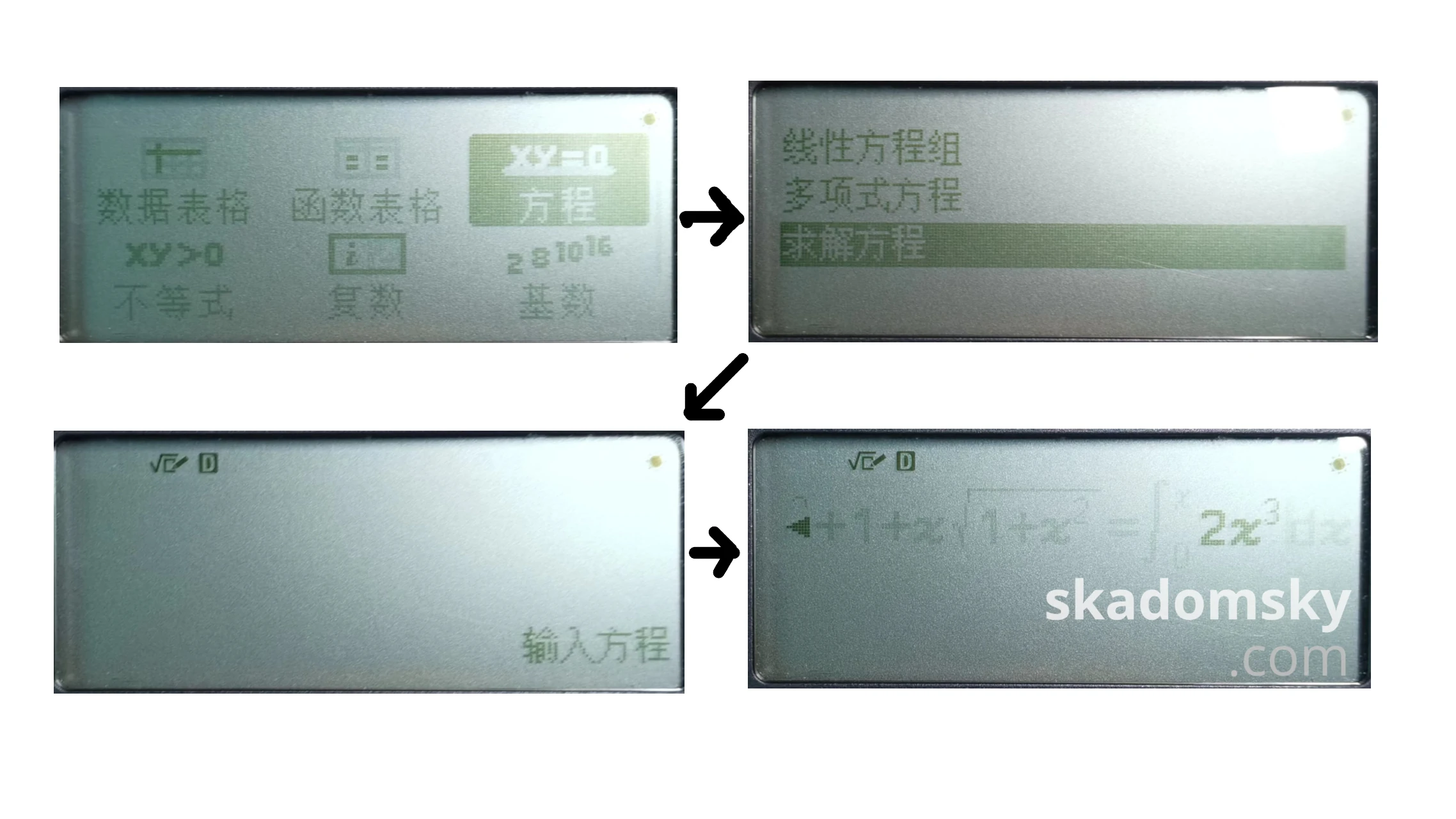
总结：
fx-999 CN CW的“求解方程”功能放宽了待解方程中不能出现一些符号的限制，不仅可以解含有积、微分符号的方程，还可以求带有排列组合、求和符号的方程。但牛顿迭代法求这类方程时，通常不太好使，因此其最大意义还是在于解定积分、微分方程。
另外，fx-999 CN CW将迭代法解方程的功能放到了“方程”模块下，似乎也具有一丝合理性，方便新用户查找功能。
小细节
翻译改进
“单位换算”菜单中，”Pressure”的翻译被更正为”压强“。
“基数”里的各进制缩写也全部翻译了。
还有一个值得注意的点是，进入“方程”模式，可以看到fx-999 CN CW不再将”Simul Equation”机械地译作“联立方程”。严格地来说，联立方程（simultaneous equations）即方程组（system of equations）是指两个及两个以上含有多个未知数的方程联立得到的组合，而线性方程特指n元一次方程组，学过线性代数的学生也更容易理解。显然后者更贴近实际情况。
科学常数改动
fx-999 CN CW内置的科学常数数值来源于CODATA 2018年的推荐值，而2014年发布的fx-991 CN X则使用2010年的推荐值。这个数值算是象征性地更新了一下，大多数考生应该使用试卷上给出的数值。
M+、M-被取消
该功能的移除并不意外。现在市面上的科学计算器基本都支持括号运算、变量存取。相比之下，记忆加（减）这个普通计算器上常见的功能就没有什么存在的必要性了。
删去记忆加（减）功能后，原来的变量$M$被重新命名为$z$，真是不留一点痕迹。
输入的细小差异
前文已经提到，fx-999 CN CW输入定积分和求和各参数的顺序较前代发生了改变。在fx-991 CN X上，按下积分键后，光标自动移至输入公式的区域。输入完公式以后按下右键，光标会移到积分的上限区域。但在fx-999 CN CW上，输入完公式后按下右键，就退出了定积分内部的编辑。
而当光标在积分左方时，按下右键，fx-991 CN X便自动将光标移至输入公式的地方，而fx-999 CN CW则是将其移到了积分的上限。虽然两台计算器在数学输入顺序方面上存在细微的差异，但线性输入各参数的顺序不受影响。
函数表格变化
函数表格比起先前的版本，操作上有了较大的改动。进入“函数表格”，fx-999 CN CW不会像fx-991 CN X一样要求用户先定义函数解析式，而是选择直接调用“功能”菜单里的函数设置。
fx-999 CN CW的函数表格可以随意地更改其中的自变量数值，估计是为了弥补删去的CALC功能。新的函数表格也可以像fx-991 CN X一样根据解析式生成固定步长和范围的表格，通过“工具”里的“表格范围”菜单即可调用。
总结
从fx-991 ES PLUS，到fx-991 CN X，再到如今的fx-999 CN CW，都是朝着用户友好的目标不断奋进。对比前代，fx-999 CN CW操作上简化了很多，可谓是做到了傻瓜机，几乎不需要成本就能快速上手。这使得新手能够快速发现计算器上的功能，让用户感到自己购买的商品物超所值，也许是销售策略中的其一。
虽然fx-999 CN系列是为“社会人士”所设计的，但主要使用人群肯定还是学生党。科研工作者有Matlab、Mathematica等运行在计算机上的高性能分析系统做支撑，金融人士有专门的金融计算器使用，普通的商贩用普通型计算器就能解决营收计算。只有在少数情况下社会人士需要使用一台函数计算器，如参加考试。fx-999 CN系列首次引入外版机中分布和数据表格的功能。在这些新功能的加持下，考生可以在考场上节约一定的时间。
就购买建议而言，fx-999 CN CW较上一代进步还是很大的，能够裸解积分、微分方程。如果有相关需求的完全可以考虑CN CW系列（包括fx-991 CN CW）。但fx-991 CN X过去十年已经深耕市场，对于一些熟悉fx-991 CN X的竞赛学生来说，适应fx-999 CN CW需要花费一定的时间成本。如果所参加的比赛未指定CW系列机型，需要慎重考虑。